
- #Haskell lambda calculus interpreter how to#
- #Haskell lambda calculus interpreter update#
- #Haskell lambda calculus interpreter full#
We find that the interpreter does implement the expected result. Now let us see what our interpreter actually implements.ĮvalCBN (EApp (EAbs (Id "x") (EAbs (Id "x") (EVar (Id "x")))) (EVar (Id "a"))) = - line 6ĮvalCBN(subst (Id "x") (EVar (Id "a")) (EAbs (Id "x") (EVar (Id "x")))) = - line 22ĮvalCBN(EAbs (Id "y") (subst (Id "x") (EVar (Id "a")) (EVar (Id "y")))) = - line 16ĮvalCBN(EAbs (Id "y") (EVar (Id "y"))) = - line 8 **Activity:** Discuss which of the two possible choices is taken in the programming languages you know. This makes a difference, because in the first case $(\lambda x.\lambda x. $$(\lambda \color$ is bound by the red or by the blue one. Our next example is $(\lambda x.\lambda x. We will continue this on Thursday, but try to do similar examples yourself before. Then, for the pattern matching my eyes only need to be able to identify what the "variable", the "argument" and the "body" are in the term at hand. For example, the equation of `line 6` I remember as "substitute the variable by the argument in the body". **Tip:** It is easier to apply an equation if one has an English phrase for it. x) a$$ Following the steps specified in the interpreter, we compute (line numbers refer to ()):ĮvalCBN (EApp (EAbs (Id "x") (EVar (Id "x"))) (EVar (Id "a"))) = - line 6ĮvalCBN (subst (Id "x") (EVar (Id "a")) (EVar (Id "x"))) = - line 15 We do some computations by hand to convince ourselves that the substitution function `subst` is doing its job. In the following we will execute the interpreter pen-and-paper, both using concrete syntax and abstract syntax. This semantics has been implemented by (). Mathematically, the semantics of $\lambda$-calculus is given by the $\beta$-rule, which is to say, by capture avoiding substitution.
#Haskell lambda calculus interpreter how to#
If you know the order of operations and how to translate concrete syntax to ASTs, you don't need to make a detour via CSTs. If you want to design your own grammar, you need to understand CSTs in order to get the order of operation right. Why do I need to understand what a CST is? The parser creates first a CST and then turns it into an AST. What are they for then?ĬSTs are an intermediate representation used by the parser. But I remember there was also sth like concrete syntax trees. The AST is used by the interpreter to evaluate (=run=execute) the program. The parser is needed to turn a program into its AST. The grammar is needed to generate the parser. For readability, in the following, it is tempting to abbreviate these trees as inīut it is safer to do this only after we gained some practice. TestLambdaNat` gives us the linearized AST Parsing this program via `echo "(\ x.x)a" |. The $\lambda$-caclulus term $(\lambda x.x) a$ is written in our programming language LambdaNat as `(\x.x)a`. We review one example to remind us of the relevant notation. how our Haskell implementation of the interpreter for $\lambda$-calculus works. to execute by hand $\lambda$-calculus programs according to its operatial semantics the formal definition of capture avoiding substitution

#Haskell lambda calculus interpreter full#
Refer back to the earlier parts of these lecture notes for full detail. Thus our interpreter actually runs more than plain lambda.
#Haskell lambda calculus interpreter update#
Quite some material has accumulated, so I here summarize some salient points and then discuss the interpreter in more detail. These on-demand lookups and the way we update env means recursive let definitions are possible.

It also helps impose referential transparency.# Interpreting Lambda Calculus Pen-and-Paper this helps prevent cheating and defining recursive functions. All definitions in the language are immutible. Once something is defined, it cannot be changed. This is called lazy evaluation or normal order evaluation, as opposed to eager or applicative order evaluation. The last line returns true because Lambda Light substitutes a variable for it's relevant binding only when it is being called, instead of when it is an argument to a function. Λ: not := \b.b false true - Lambda Light allows you to create functions with named functions. Λ: false := \x.\y.y - Lambda Light supports bindings to a global namespace. Λ: true := \x.\y.x - Lambda Light supports binding names to expressions. Λ: (λx.x x) (λx.x) - Lambda Light supports function application.
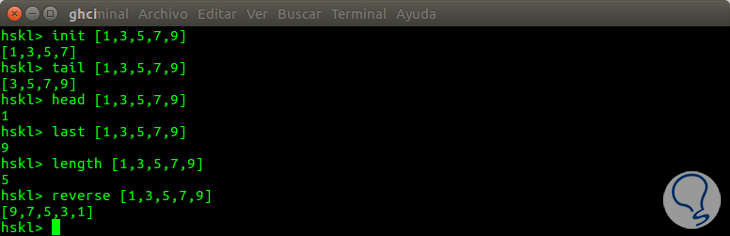
Λ: \x.x - Lambda Light supports the creation lambda expressions using \ and the unicode λ character. Λ: x - Lambda Light supports creating arbitrary variables. Λ: - Lambda Light supports Haskell-like single line comments


 0 kommentar(er)
0 kommentar(er)
